Supplementary Box 1: Functional classes of cells and learning: Simple and complex cells.

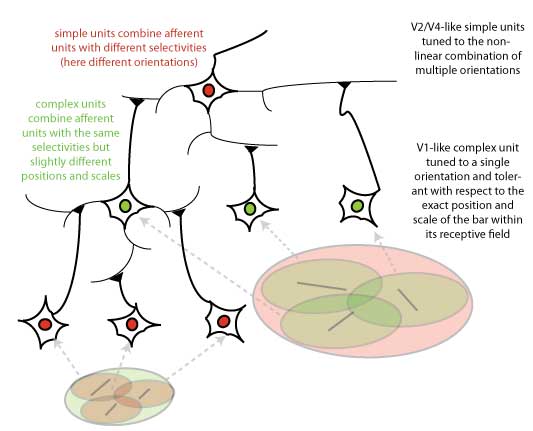
Following their work on striate cortex [1], Hubel & Wiesel first described two classes of functional cells. Simple cells that respond best to bar-like (or edge-like) stimuli at a particular orientation, position and phase (i.e., white bar on a black background or dark bar on a white background) within their relatively small receptive fields. Complex cells, on the other hand, while also selective for bars, tend to have larger receptive fields (about twice as big) and exhibit some tolerance with respect to the exact position (and phase of the bar) within their receptive fields. Hubel & Wiesel described a way by which specific pooling mechanisms could explain the response properties of these cells.

Simple-cell-like receptive fields could be obtained by pooling the activity of a small set of cells tuned to spots of lights (as observed in ganglion cells in the retina and the Lateral Geniculate Nucleus) aligned around a preferred axis of orientation (not shown on the figure). Similarly, position tolerance at the complex cell level (green color on the figure), could be obtained by pooling over afferent simple cells (at the level below) with the same preferred orientation but slightly different positions.

Recent work has provided evidence for such selective pooling mechanisms in V1 [2]. Extending these ideas from primary visual cortex to higher areas of the visual cortex led to a class of models of object recognition, the feedforward hierarchical models (see [3] for a recent review). Illustrated at the top of the figure on the left is a V2-like simple cell obtained by combining several V1 complex cells tuned to bars at different orientations. Iterating these selective pooling mechanisms leads to a hierarchical architecture like the one described in Figure 2. Along the hierarchy, units become selective for increasingly complex stimuli and at the same time exhibit more and more invariance properties with respect to position (and scale). Learning of selectivity and invariance.

In the model of Figure 1, simple units are selective for specific conjunctions of inputs (i.e., similar to an and-like operation). Their wiring thus corresponds to learning correlations between inputs at the same time-points (i.e., for simple cells in V1, the bar-like arrangements of LGN inputs, and beyond V1, more elaborate arrangements of bar-like subunits, etc). This corresponds to learning what combinations of features appear most frequently in images (i.e., which sets of inputs are consistently co-active) and to become selective to these patterns. Conversely the wiring of complex units may correspond to learning how to associate frequent transformations in time – such as translation and scale – of specific image features coded by afferent (simple) cells. The wiring of the complex units reflects learning of correlations across time (because of the object motion), e.g., for V1-like complex units, learning which afferent units with the same orientation and neighboring locations should be wired together because, often, such a pattern changes smoothly in time (under translation) [4].

[1] Hubel, D. H. and Wiesel, T. N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol, 160, (Jan 1962), 106-154.

[2] Rust, N., Schwartz, O., Simoncelli, E. P. and Movshon, J. A. Spatiotemporal elements of macaque V1 receptive fields. Neuron, 46, 6 (Jun 16 2005), 945-956.

[3] Serre, T., Kouh, M., Cadieu, C., Knoblich, U., Kreiman, G. and Poggio, T. A theory of object recognition: computations and circuits in the feedforward path of the ventral stream in primate visual cortex. MIT AI Memo 2005-036 (2005).

[4] Foldiak, P. Learning invariance from transformation sequences. Neural Comp, 3, (1991), 194-200.

Supplementary Note: Computational models of the visual cortex

Feedforward hierarchical models have a long history starting with Marko & Giebel’s homogeneous multi-layered architecture [1] in the 70’s and later Fukushima’s Neocognitron [2]. One of the key computational mechanisms in these, and other hierarchical models of visual processing, originates from the pioneering physiological studies and models of Hubel and Wiesel.

The basic idea in these models is to build an increasingly complex and invariant object representation in a hierarchy of stages by progressively integrating (i.e., pooling) convergent inputs from lower levels. Building upon several existing neurobiological models [3-9], conceptual proposals [10-13] and computer vision systems [2, 14], we have been developing [5, 15] (see also [16, 17]) a similar computational theory that attempts to quantitatively account for a host of recent anatomical and physiological data.

[1] Marko, H. and Giebel, H. Recognition of handwritten characters with a system of homogeneous Layers. Nachrichtentechnische Zeitschrift, 231970), 455-459.

[2] Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cyb., 361980), 193-202.

[3] Wallis, G. and Rolls, E. T. A model of invariant recognition in the visual system. Prog Neurobiol, 511997), 167-194.

[4] Mel, B. W. SEEMORE: Combining color, shape and texture histogramming in a neurally-inspired approach to visual object recognition. Neural Comp., 9, 4 1997), 777-804.

[5] Riesenhuber, M. and Poggio, T. Hierarchical models of object recognition in cortex. Nature Neuroscience, 2, 11 1999), 1019-1025.

[6] Ullman, S., Vidal-Naquet, M. and Sali, E. Visual features of intermediate complexity and their use in classification. Nat Neurosci, 5, 7 (Jul 2002), 682-687.

[7] Thorpe, S. Ultra-Rapid Scene Categorization with a Wave of Spikes. In Proceedings of the Workshop on Biologically Motivated Computer Vision (BMCV) (2002).

[8] Amit, Y. and Mascaro, M. An integrated network for invariant visual detection and recognition. Vision Research, 43, 19 2003), 2073–2088.

[9] Wersing, H. and Koerner, E. Learning optimized features for hierarchical models of invariant recognition. Neural Comp., 15, 7 2003), 1559–1588.

[10] Hubel, D. H. and Wiesel, T. N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol, 160, (Jan 1962), 106-154.

[11] Perrett, D. and Oram, M. Neurophysiology of shape processing. Image Vision Comput, 111993), 317-333.

[12] Hochstein, S. and Ahissar, M. View from the top: hierarchies and reverse hierarchies in the visual system. Neuron, 36, 5 (Dec 5 2002), 791-804.

[13] Biederman, I. Recognition-by-Components: A Theory of Human Image Understanding. Psych. Rev., 941987), 115–147.

[14] LeCun, Y., Bottou, L., Bengio, Y. and Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. of the IEEE, 86, 11 1998), 2278–2324.

[15] Serre, T., Kouh, M., Cadieu, C., Knoblich, U., Kreiman, G. and Poggio, T. A theory of object recognition: computations and circuits in the feedforward path of the ventral stream in primate visual cortex. MIT AI Memo 2005-036 / CBCL Memo 259, AI Memo 2005-036 / CBCL Memo 259 2005).

[16] Mutch, J. and Lowe, D. Multiclass Object Recognition Using Sparse, Localized Features. In Proceedings of the CVPR (2006).

[17] Masquelier, T., Serre, T., Thorpe, S. and Poggio, T. Learning complex cell invariance from natural videos: a plausibility proof. CBCL Paper #269/MIT-CSAIL-TR #2007-0602007).