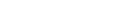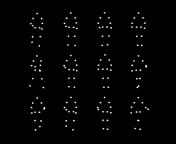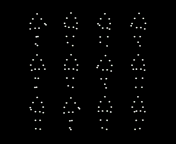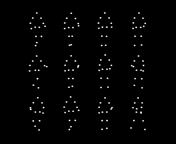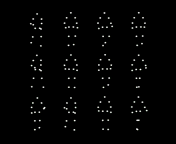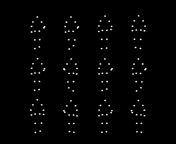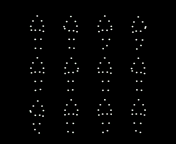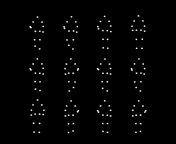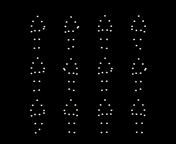The goal of this project is to study the pre-attentive ensemble coding mechanisms consistent with feedforward hierarchical models of visual processing. In recent work,
we extend a biological model of motion processing with a new dictionary learning
method tailored for crowd perception [HBU2014@ECCV]. Our approach uses a
sparse coding model to learn crowd prototypes. Ensemble coding mechanisms are
implemented via structural and local coherence constraints. We evaluate the
proposed method on multiple crowd perception problems from collective or
abnormal crowd detection to tracking individuals in crowded scenes.

Motivation

Typically, one of the main limitations with traditional methods is that they focus on
modeling local motion patterns when patterns of crowd behavior tend to be more
global. As a result the underlying crowd representation tends to be relatively
unstable and fail to capture typical crowd peculiarities. We conduct examples in on
the below figure like local and unstable codes, we try to get global and prototypical
codes.

Fig. 1. Illustrative example demonstrating that crowd patterns are difficult to learn with basic sparse coding (left). Patterns of crowd behavior tend to be complex and difficult to represent using only local rules. In this work, we build a feedforward hierarchial models for crowd perception using a novel sparse prototype learning method (right), which incorporates structural and coherence constraints to learn richer, more meaningful, crowd patterns.

Cognitive Psychology Background

Fig. 2. People are more accurate at reporting the mean direction rather than any
individual person (check what they actually do) etc. Such results have been taken as
suggestive evidence that observers rapidly pool motion, orientation or speed
information from multiple walkers to estimate the movement of a crowd [23] (Top).
During rapid presentations, human observers seem to estimate the mean value of
the intended direction of crowds as point-light walkers rather than individual
walkers briefly (Bottom). It is very much in the spirit of feedforward hierarchical
models [10].

Insight for crowd perception

Motivated by these biological considerations, we propose a significant extension of
a feedforward hierarchical model of the visual cortex from the recognition of
individual behaviors to group behaviors. Crowd prototypes are learned as mid-level
representation of the motion processing hierarchy based on a sparse coding model.
The proposed optimization learns crowd prototypes through ensemble coding
mechanisms by jointly enforcing local structure and coherence in the input motion
patterns.

Overall architecture

The model starts with motion-sensitive simple (S1) and complex (C1) units similar to
simple and complex cells found in the primary visual cortex. Specifically, we build a
population of motion-sensitive simple (S1) units tuned to both speed and motion
direction using the optical flow estimated from local space-time 3D volumes. In
subsequent processing stages, units of higher visual complexity emerge after an
additional template-matching (S2 units) as well as an invariance-pooling (C2 units)
stage, increasing both the selectivity and invariance properties of the underlying
model units. The response of S2 units is obtained by convolving C1 maps across all
motion directions with a dictionary of stored prototypes. Originally, the dictionary of
K S2 prototypes is learned via a simple random sampling procedure. Here, instead,
we propose to learn crowd prototypes via sparse coding methods.

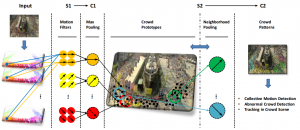
Fig. 3. Sketch of the proposed hierarchal model for crowd perception.

Crowd prototypes learning

(1) Sparse Coding Based Crowd Prototypes

Given a set of N input vectors R, learning a sparse dictionary of coding elements can
be formulated as the following optimization problem: where B is a matrix that
contains the learned basis functions as column vectors and S is a matrix containing
the corresponding linear coefficients. We propose to incorporate the idea of
ensemble coding in the form of two additional penalty terms.

(2) Object function with penalty terms

• Structural neighborhood cohesion term: forces input patterns to converge towards a similar interpretation.
• Neighborhood manifold coherence term: incorporates explicit pooling mechanisms over output vectors to yield a locally more stable code.

Because this objective function is not convex with respect to R, B and S, we use a
two-alternative minimization approach, alternatively optimizing one variable while
fixing the others. We formulate the coherence constraint as a graph-based Laplacian
regularization problem and the structural constraint as a generalized Tikhonov
regularization problem.

(a) Illustrative results on the Marathon sequence for the first 5 iterations (from left
to right).

(b) Comparison between different methods for prototype learning on the Marathon
sequence using the same number of prototypes. From left to right: standard
optical flow, basic sparse coding, graph-based sparse coding, proposed crowd
prototype learning.
Fig. 4. Illustration of prototypes for 5 iterations.

Experiments

Abnormal event detection

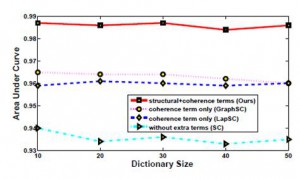
Fig. 5. Evaluation of the different penalty terms used in the proposed optimization function.

Table 1. AUC measures for the detection of abnormal behavior on the UMN dataset.

Collectiveness classification

Fig. 6. Representative examples of the learned prototypes. Shown are sample frames
from the Collective Motion Dataset [35] overlaid with color coded symbols (best
seen in color) indicating the closest prototype for the corresponding location.

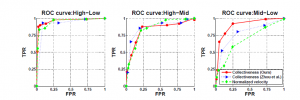
Fig. 7. ROC curves for the classification of collectiveness levels. We compare a
“prototype” score P derived using the proposed approach with a “collectiveness”
score C and the “normalized velocity” V (see text for details).

Tracking in Crowded Scene

Fig. 8. Tracking results on 3 sequences for comparison between the proposed
approaches (circles) vs. the approach by Zhang et al [29] (squares). The ground truth
is shown with dots. Tracking results for different subjects are marked with different
colors.

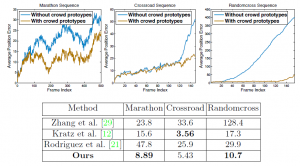
Fig. 9. Top: Average position error curves for the proposed sparse coding approach
and comparison with baseline. Bottom: Comparison between tracking approaches
using the average position error computed over entire sequences.

Relevant publication

[HBU2014@ECCV] Yanhao Zhang, Shengping Zhang, Qingming Huang, Thomas Serre.
Learning Sparse Prototypes for Crowd Perception via Ensemble Coding Mechanisms.
5th International Workshop on Human Behavior Understanding

Additional references

[3] Cong, Y., Yuan, J., Liu, J.: Sparse reconstruction cost for abnormal event detection.
In: CVPR (2011)

[5] Cui, X.and Liu, Q., Gao, M., Metaxas, D.: Abnormal detection using interaction
energy potentials. In: CVPR (2011)

[10] Jhuang, H., Serre, T.,Wolf, L., Poggio, T.: A biologically inspired system for action
recognition. In: ICCV (2007)

[12] Kratz, L., Nishino, K.: Tracking with local spatio-temporal motion patterns in
extremely crowded scenes. In: CVPR (2010)

[18] Mehran, R.and Oyama, A., Shah, M.: Abnormal crowd behavior detection using
social force model. In: CVPR (2009)

[19] Mehran, R. Moore, B., Shah, M.: A streakline representation of flow in crowded
scenes. In: ECCV (2010)

[21] Rodriguez, M., Ali, S., Kanade, T.: Tracking in unstructured crowded scenes. In:
ICCV (2009)

[23] Sweeny, T.D., Haroz, S., Whitney, D.: Perceiving group behavior: Sensitive
ensemble coding mechanisms for biological motion of human crowds. Journal of
experimental psychology: human perception and performance 39(2), 329 (2013)

[29] Zhang, K., Zhang, L., Yang, M.H.: Real-time compressive tracking. In: ECCV (2012)

[35] Zhou, B., Tang, X., Wang, X.: Measuring crowd collectiveness. In: CVPR (2013)